Вычисление математических функций в j2me (exp, ln, log, arcsin, arccos, arctn, power, root)

КонфигурацияCDLC 1.1 позволяет работать с вещественными числами, поддерживая типdouble. Однако стандартная библиотекаMathвключает в себя очень скудный набор математических функций:sin,cos, tan,sqrt. Существует несколько сторонних математических классов (например,Real.java, которую можно скачать по адресуhttp://sourceforge.net/projects/real-java). В этой статье я предлагаю написать собственную реализацию нескольких популярных математических функций.

В основе компьютерной математики лежит использование разложений функций в математические ряды. Подробно этот вопрос рассматривается в курсе Математического анализа любого Вуза. Если вкратце, то математическую функцию можно представить в виде бесконечной суммы слагаемых, причем каждое следующее слагаемое по модулю меньше предыдущего. Поэтому для вычисления функции с заданной точностью нужно выполнять сложение до тех пор, пока следующее слагаемое не станет меньше, чем требуемая точность вычисления.

Вычисление Экспоненты

Из курса математического анализа известно, что экспоненту можно представить в виде бесконечного ряда

.

При этом, чем больше аргументx, тем больше слагаемых требуется брать для удовлетворения требуемой точности. Приx>706exp(x) не умещается в переменную типаdouble, поэтому перед вычислением экспоненты целесообразно проверить значениеxна превышение порогового предела. Для реализации эффективного алгоритма вычисления экспоненты, нужно воспользоваться известным из курса школьной алгебры фактом:

Очевидно, числоx<706 можно представить в виде суммы:

где коэффициентыaмогут принимать значения 0 или 1, аb<1.

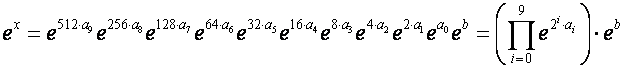
Величиныможно вычислить заранее и записать в массив. Затем вычленить изxцелую(b) и дробную часть. Для дробной части вычислить экспоненту как сумму ряда Тейлора. Найтиa_iможно, переведя целую часть числаxв двоичную систему. Тогда самому правому символу в двоичном представлении числа соответствуетa₀, второму справа числу –a₀, и так далее. Ниже приведен код функции, вычисляющей экспоненту числа:

private double MExp(double x0){
double x=x0;
if(x0<0){x=-x0;}
//Массив со степенями экспоненты.
double ExpConst[]={
2.718281828459045,//e^1
7.389056098930649,//e^2
54.59815003314422,//e^4
2980.957987041726,//e^8
8886110.520507860,//e^16
78962960182680.61,//e^32
6.235149080811582e27,//e^64
3.887708405994552e55,//e^128
1.511427665004070e111,//e^256
2.284413586539655e222//e^512
};
int x1=(int)x;//Выделяем целую часть числа
//Вычисляем экспоненту как сумму ряда Тейлора
int long n=1;
double b=1;
double sn=1;
while(sn>1E-16){
sn=sn*(x-x1)/n;
b=b+sn;
n=n++;
}
//Переводим показатель экспоненты в двоичную систему.
StringBuffer s1=new StringBuffer(10);
s1.append(Integer.toBinaryString(x1));
int len=s1.length();
for(int i=s1.length(); i>0;i--)
{
if(s1.charAt(i-1)=='1'){b=b*ExpConst[len-i];}
}
if(x0<0){b=1/b;}
return b;
}

Гиперболические функции

Имея функцию для вычисления экспоненты, легко найти значения гиперболических функций.

, , .

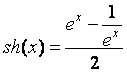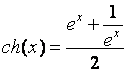Имеет смысл предварительно записать значениеexp(x) во вспомогательную переменную, которую затем использовать для вычисления по формулам.

Вычисление натурального логарифма

Натуральный логарифм можно представить в виде суммы:

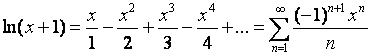
Вычислять значение логарифма непосредственно по этой формуле не очень эффективно. Для оптимизации алгоритма вычисления можно воспользоваться известными соотношениями

,

.

Представим числоxв виде

,

гдеb<1,a-целое, тогда

.

Для того чтобы представить числоxв требуемом виде, нужно найти позицию символа “E” в строковом представлении числаx, тогдаaравно числу, записанному правее символа “E” плюс 1,ab– числу записанному левее “E”, деленному на 10.

Ниже представлен код, реализующий алгоритм вычисления натурального логарифма:

private double MLn(double x0){
double x=x0;
double y=0;
//Получаем показатель степени.
String s0=""+x;
int i=s0.indexOf("E");
String s1=s0.substring(i+1, s0.length());//Правее E
String s2=s0.substring(0, i);//Левее E
double a=0,b=0;
a=Double.parseDouble(s1)+1;
b=Double.parseDouble(s2)/10;
//Вычисление Логарифма b как суммы ряда Тейлора
int n=1;
double sn=1;
while(sn>(1E-16)*n){
sn=-sn*(b-1);
y=y+sn/n;
n=n++;
}
y=y+a*2.302585092994046;
return y;
}

Вычисление корней, степеней и логарифмов

Имея функцию для вычисления натурального логарифма, легко вычислить следующие функции:

Вычисление арксинуса и арккосинуса

Вычисление обратных тригонометрических функцийarcsinи arcosсводится к вычислению рядов:

,

,

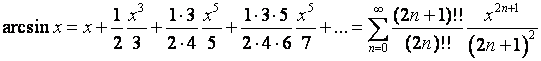Ниже приведен алгоритм вычисления арксинуса.

private double Marcsin(double x0){
double x=x0;
if(x0<0){x=-x0;}
double y=x;
int n=1;
double sn=x;
while(sn>1E-16){
sn=sn*(2+1.0/n)*0.5*x*x;
y=y+sn/(2*n+1)/(2*n+1);
n=n+1;
}
if(x0<0){y=-y;}
return y;
}
 

Вычисление арктангенса

,

Предложенная формула эффективна для вычисления арктангенса малого аргумента. Для построения алгоритма эффективного вычисления арктангенса от большихx, целесообразно воспользоваться формулой:

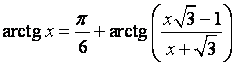
Ниже предлагается переписанный дляjavaалгоритма, который написал товарищ Nikitin V.F. в 2000 году.

1. Вначале нужно проверить знакx, если x<0, нужно изменить знак, сделав аргумент неотрицательным.
2. Затем еслиx>1, обратить его:x=1/x.
3. Затем сокращаем область определения (запоминая число сделанных шагов), используя формулу:

до тех пор, покаxне окажется в интервале [0,pi/12].

4. После этого можно вычислятьy=arctg(x) по формуле Тейлора.
5. Сместим результатyнаp/6 необходимое число раз
6. Еслиxбыло больше 1, то результат
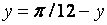
7. Еслиxбыло отрицательным, то результат

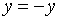
private double MArctg(double x0){
int sp=0;
double x,x2,y;
x=x0;
if(x<0){x=-x;}
if(x>1){x=1.0/x;}
//Уменьшаем интервал области аргумента
while(x>0.2617993877991495){
sp++;//Вспомогательный счетчик шагов
x=(x*1.732050807569-1)/(x+1.732050807569);
}
//Вычисляем ряд Тейлора
y=x;
int n=1;
double sn=x;
while(sn>1E-16){
sn=sn*(2+1.0/n)*0.5*x*x;
y=y+sn/(2*n+1)/(2*n+1);
n=n+1;
}
 
//Смещаем все на pi/6 необходимое число раз
y=y+sp*0.523598775598
 
if(x0>1) a=0.2617993877991495-a;
if(x0<0) y=-y;
 
return y;
}

Автор:Александр Ледков (aRix).