Поворот изображения на произвольный угол в J2ME MIDP 2.0

При разработки игр, часто бывает необходимо повернуть изображение на какой-либо угол. К сожалению, стандартные средства J2ME позволяют осуществлять поворот только на угол кратный 90 градусам. Из этой ситуации можно выкрутиться, подготовив набор рисунков в интервале от нуля до 90 градусов и поворачивая их на 90, 180 или 270 градусов. Таким образом можно обеспечить плавное вращение картинки. Этот способ не очень хорош, поскольку размер приложения увеличится во много раз. В этой статье я предлагаю рассмотреть альтернативный способ.

MIDP 2.0 позволяет работать с изображением, представленным в виде массива точек (ARGB массива). Более подробно о работе с ARGB массивами можно узнать из статьи: www.mobilab.ru/articles/75. Разобьем нашу задачу на несколько частей.

1. Загрузка исходного изображения в ARGB массив.
2. Поворот изображения, хранящегося в ARGB массиве, на заданный угол
3. Вывод полученного изображение на экран.

Загрузка изображения в ARGB массив

Для начала нам нужен рисунок. Я особо не забивал голову и взял первое, что попалось под руку.

Загрузим этот рисунок в нашу программу:

private Image image1;
…
try{
image1= Image.createImage("/1.png");
}
catch(java.io.IOException io){}

Теперь перегоним его в ARGB массив. Целесообразно создать два массива. В одном Мы будем хранить исходное изображение (ARGB_Img0), а в другом - повернутое на необходимый угол (ARGB_Img1). Я работал с квадратным рисунком. Думаю, Вы без труда адаптируете мою программу для работы с картинкой произвольного размера.

//Объявляем два массива
private int ARGB_Img[],ARGB_Img2[];
…
 
//Определяем размер исходной картинки
ImW=image1.getWidth();//Ширина
ImH=image1.getHeight();//Высота
//Создаем два ARGB массива
ARGB_Img0=new int[ImW*ImH];
ARGB_Img1=new int[ImW*ImH];
//Загружаем в первый массив нашу картинку.
image1.getRGB(ARGB_Img,0,ImW,0,0,ImW,ImH);

Поворот изображения

Если Вы решили заняться компьютерной графикой, Вам не обойтись без линейной алгебры. Я не буду вдаваться в подробности и объяснять, как я получил формулы преобразований, а просто скажу, что для каждой точки массива ARGB_Img1 я по приведенным ниже формулам нахожу соответствующую точку массива ARGB_Img0. Само преобразование представляет собой перенос и поворот системы координат на заданный угол.

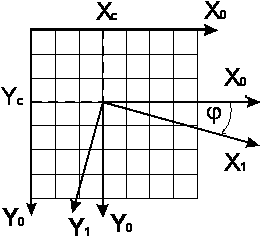
Формулы преобразований имеют вид:

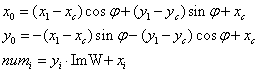
Здесь x0,y0 – координаты точки в ARGB_Img0, x1,y1 – координаты точки в ARGB_Img1, xc,yc – координаты центра поворота в системе координат x0y0, numi – позиция точки (xi,yi) в ARGB_Imgi массиве.

Вынесем код, связанный с поворотом в отдельную процедуру.

public void ARGB_Img_rot(int phi)
{
int x0,y0,x1,y1;
int sn=sin(phi);
int cs=cos(phi);
for(y1=0;y1<ImH;y1++){
for(x1=0;x1<ImW;x1++)
{
//На всякий случай заполняем картинку цветом фона
ARGB_Img1[y1*ImW+x1]=bgcol;
x0=(int)((cs*(x1-xc)+sn*(y1-yc))/1000+xc);
y0=(int)(-(sn*(x1-xc)-cs*(y1-yc))/1000+yc);
//Проверяем, не выходит ли точка за пределы области
if(x0>-1)
if(x0<ImW)
if(y0>-1)
if(y0<ImH)
{//Закрашиваем точку
ARGB_Img1[y1*ImW+x1]=ARGB_Img0[y0*ImW+x0];
}
}
}
}

Мы столкнулись с одной проблемой. В формулы входят sin и cos, но J2ME ничего о них не знает. Нам придется вручную написать эти функции. Воспользуемся дедовским способом, известным еще со времен первого Doom–а и Wolf 3D – снабдим наше приложение таблицей синусов. Для этого создадим два массива:

private int alpha[]={0,10,20,30,40,50,60,70,80,90};
private int sin_t[]={0,174,342,500,643,766,866,940,985,1000};

В массив alpha занесем углы (обратите внимание на постоянный шаг), а в sin_t – соответствующие им значения синуса. Мы не случайно ограничились промежутком от 0 до 90 градусов и не создали такую же таблицу для косинусов. Известные всем формулы приведения позволяют легко получить синусы и косинусы любых углов, если известен синус на промежутке [0;90]. Еще одна особенность массива sin_t – это то, что все значения умножены на 1000 и округлены до целых частей. Если Вы посмотрите на формулы преобразований в ARGB_Img_rot(), то поймете, зачем это сделано.

Итак, у нас есть значения синуса в узловых точках, но как определить его значения между ними, например, для угла 26 градусов? Можно просто брать наиболее близкое из записанных в таблице значений, можно использовать сплайны или линейную интерполяцию. Я воспользуюсь последним способом, поскольку он дает неплохую точность и требует немного ресурсов.

Для начала нужно определить, между какими двумя узлами находится требуемый угол. Зная, что шаг в таблице равен 10 градусам, я просто делю угол на десять и отбрасываю дробную часть, получая таким образом номер левого узла. Затем я беру следующий узел и по линейному закону определяю значение в интересующей меня точке.

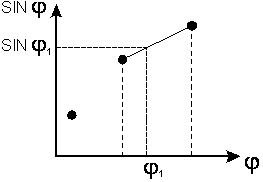
public int sinus(int t)
{
int k;
k=(int)(t/10);
if(t%10==0)
{
return sin_t[k];
}
else{
return(int)((sin_t[k+1]-sin_t[k])*(t%10)/10+sin_t[k]);
}
}

Теперь, когда у нас есть функция, возвращающая значение синуса на промежутке от 0 до 90 градусов, мы легко можем написать функции sin и cos для произвольного угла

public intsin(int t)
{
int sign=1;
t=t%360;//Учтем период синуса
if(t<0)//Учтем нечетность синуса
{
t=-t;
sign=-1;
}
//Воспользуемся формулами приведения
if(t<=90){return sign*sinus(t);}
elseif(t<=180){return sign*sinus(180-t);}
elseif(t<=270){return-sign*sinus(t-180);}
else{return-sign*sinus(360-t);}
}
 
public intcos(int t)
{
t=t%360;//Учтем период синуса
if(t<0){t=-t;}//Учтем четность косинуса
//Воспользуемся формулами приведения
if(t<=90){return sinus(90-t);}
elseif(t<=180){return-sinus(t-90);}
elseif(t<=270){return-sinus(270-t);}
else{return sinus(t-270);}
}
 
Все готово. Осталось вывести рисунок на экран.
 
public void paint(Graphics g)
{
g.setColor(150,150,150);
//Очищаем экран
g.fillRect(0,0,GrW,GrH);
 
g.drawImage(image1,10,10,Graphics.TOP|Graphics.LEFT);
g.drawRGB(ARGB_Img1,0,ImW,10,20+ImH,ImW,ImH,false);
g.drawRGB(ARGB_Img1,0,ImW,20+ImW,10,ImW,ImH,true);
}

Результат работы программы приведен ниже.

Можете скачатьфайлы с исходниками моего приложения иготовую программу.

Автор:Александр Ледков (aRix).