Рисование линий произвольной толщины в Java2ME
Набор графических функций включенных в MIDP 2.0 достаточно сильно ограничен, в отличии от большинства настольных операционных систем, в нем отсутствует понятие кисти рисования, поэтому линии рисуются толщиной в один пиксель с одним типом пунктира. При выводе векторных данных, таких например, как карты, часто появляется задача нарисовать линию произвольной толщины. Статья, представленная вашему вниманию, посвящена одному из вариантов решения данной проблемы.
Для рисования линии заданной толщины есть несколько непересекающихся методов, первый и самый корректный - это рисование линии точками по одному из стандартных алгоритмов, плюсы данного метода в том, что можно написать универсальную процедуру рисования линии любой фактурой и цветом (линия из узора), минусом является низкая скорость построения линии, что для мобильных устройств непростительно. Второй вариант очень быстрый, но позволяет рисовать только линии залитые сплошной фактурой, при его использовании рассчитываются координаты крайних точек линии, после чего она рисуется выводом двух залитых треугольников. Именно этот вариант мы и рассмотрим.
Для начала небольшой экскурс в аналитическую геометрию, попрошу математиков сильно не смеяться ;). Для построения прямоугольника, представляющего нашу будущую линию необходимо определить координаты четырех точек прямоугольника, при этом нам известны координаты концов линии и ее толщина. Все это проиллюстрировано рисунком ниже:
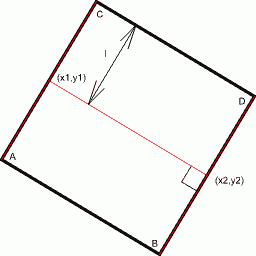
Итак нам известны координаты (x1,y1) (x2,y2) и толщина линии l. Для определения координат точекA иC нам необходимо найти уравнения задающие прямую проходящую через точку с координатами (x1,y1) и перпендикулярную прямой соединяющей точки (x1,y1) (x2,y2). Для начала находим направляющий вектор, параллельный заданной прямой, проходящей через (x1,y1) (x2,y2)
A=x2-x1 B=y2-y1 S(A,B)=S(x2-x1,y2-y1)
а теперь записываем уравнение прямой проходящей через точку (x1,y1) и перпендикулярную векторуS(A,B) в параметрической форме
x=B*t x1 y=-A*t y1
теперь для получения координат точекA и C достаточно подставить в уравнение положительный и отрицательный параметрt, к несчастью, этот параметр ни к чему не привязан, поэтому выполним его нормирование. Так как уравнение линейное - достаточно получить всего одну точку на прямой, для этого подставим в уравнения прямой вместо параметра произвольное число (например единицу), определим координату точки и найдем расстояние от этой точки до точки (x1,y1). После преобразований получим расстояние
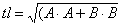
Теперь мы можем выполнить нормирование параметраt, определив какой длине отрезка соответствует единица параметра, разделив единицу на tl. Так как у нас задана толщина линии, то умножив ее на коэффициент нормирования мы получим значение параметра для данной толщины линии. Для нахождения координат точек A и C достаточно подставить в параметрическое уравнение прямой положительный и отрицательный параметр. Координаты точекB иD находятся аналогично, только в параметрические уравнения вместоx1, y1 подставляютx2 иy2.
На этом математическая часть закончена - приступим к реализации на Java2ME. Как мы видим из формул выше, нам понадобится реализация функции квадратного корня. Недолго думая, используем классический вариант с расчетом по формуле Ньютона, реализованной в виде функции sqrt:
public intsqrt(int l) { int ret=l;int div=l; if(l<=0)return0; while(true) { div=(l/div div)/2; if(ret>div)ret=div;elsereturn ret; } }
Теперь осталось реализовать готовый алгоритм. На вход процедуре подается контекст графического экранаg, две пары координат - начальная (x1,y1) и конечная (x2,y2) точки, ширина линии w. В первом приближении реализация выглядит так:
public void fillLine(Graphics g,int x1,int y1,int x2,int y2,int w) { int a,b,l; a=(x2-x1);b=(y2-y1); l=sqrt(b*b a*a); a=a*w/l;b=b*w/l; g.fillTriangle(b x1,y1-a,x1-b,a y1,b x2,y2-a); g.fillTriangle(x2-b,a y2,x1-b,a y1,b x2,y2-a); }
В этом случае линия рисуется симметрично исходным координатам, но ее реальная толщина будет равна удвоенному параметру плюс единица, в результате, при параметре толщины 1 пиксель будет нарисована линия толщиной 3 пикселя, а при заданной толщине 2 рисуется линия толщиной 5 пикселей. Теперь достаточно принять решение как будут рисоваться линии с шириной кратной двум. Так как мы имеем дело с пикселями - единственный метод - это рисовать одну из симметричных сторон на единицу меньшей толщины. Линии при этом получаются не симметричные относительно заданных координат, но другого способа растеризовать прямую нет ;(. В алгоритм придется внести несколько изменений. Так как у нас все расчеты идут в целочисленной форме, одна половинка (от точки x1,y1 до точкиC) будет иметь длину l1=bold/2, а вторая (от точки x1,y1 до точкиA), с учетом того, что линия x1,y1-x2,y2 имеет толщину в один пиксель l2=bold-bold/2-1. Реализация от этого изменится не намного:
public void fillLine(Graphics g,int x1,int y1,int x2,int y2,int w) { int a,b,l; a=(x2-x1);b=(y2-y1); l=sqrt(b*b a*a); g.fillTriangle(b*w/2/l x1,y1-a*w/2/l,x1-b*(w-(w/2)-1)/l,a*(w-(w/2)-1)/l y1,b*w/2/l x2,y2-a*w/2/l); g.fillTriangle(x2-b*(w-(w/2)-1)/l,a*(w-(w/2)-1)/l y2,x1-b*(w-(w/2)-1)/l,a*(w-(w/2)-1)/l y1,b*w/2/l x2,y2-a*w/2/l); }
Данный алгоритм работает достаточно хорошо, но не без недостатков, в первую очередь это связано с тем что при рисовании залитых треугольников небольшой толщины их край рисуется пунктиром, поэтому линии с толщиной в одну-две точки будут выводиться пунктиром. Решается эта проблема легко - введением проверки на заданную толщину линии. Так как все расчеты ведутся в целых числах, то для повышения точности расчетов введем округление вида. y=(5 x*10)/10, кроме того увеличим точность расчета квадратного корня, умножив его аргумент на 100 и разделив в итоге результат на 10. Так как расчет каждой координаты все удлиняется введем новые переменные lx1,lx2,lx3,lx4,ly1,ly2,ly3,ly4, представляющие собой координаты точекA, B, C, D - потеряв в памяти но выиграв в скорости. Результат приведен ниже:
public void fillLine(Graphics g,int x1,int y1,int x2,int y2,int w) { if(w==1)g.drawLine(x1,y1,x2,y2);else{ int a,b,l,lx1,lx2,lx3,lx4,ly1,ly2,ly3,ly4; a=(x2-x1);b=(y2-y1); l=sqrt(100*(b*b a*a)); lx1=(5 b*100*w/2/l x1*10)/10; ly1=(5 y1*10-a*100*w/2/l)/10; lx2=(5 b*100*w/2/l x2*10)/10; ly2=(5 y2*10-a*100*w/2/l)/10; lx3=(5 x1*10-b*100*(w-(w/2)-1)/l)/10; ly3=(5 a*100*(w-(w/2)-1)/l y1*10)/10; lx4=(5 x2*10-b*100*(w-(w/2)-1)/l)/10; ly4=(5 a*100*(w-(w/2)-1)/l y2*10)/10; g.fillTriangle(lx1,ly1,lx3,ly3,lx2,ly2); g.fillTriangle(lx4,ly4,lx3,ly3,lx2,ly2); }}
Добавив округление ко всем координатам, мы опять столкнемся с особенностью прорисовки края залитого треугольника в J2ME, когда при малой толщине треугольника, его край рисуется не полностью, уменьшая его видимую ширину. Простейший способ это устранить - добавить рисование линий по контуру толстой прямой, соединив точкиABCD. После этого проявится другой эффект, когда линии с наклоном близким к вертикали рисуются толще на один пиксель. Поэтому линии соединяющие точки ABCD будем рисовать только при наклоне до 45 градусов по вертикали, для этого используем проверку (Math.abs(a)>Math.abs(b)). Добавим в конец предыдущего примера рисование граничных линий:
if(Math.abs(a)>Math.abs(b)){ g.drawLine(lx1,ly1,lx2,ly2); g.drawLine(lx3,ly3,lx4,ly4); g.drawLine(lx4,ly4,lx2,ly2); g.drawLine(lx1,ly1,lx3,ly3); }
Все работает нормально, но при рисовании горизонтальных или вертикальных линий все равно видно, что толщина выдерживается не всегда, проверка показывает, что это происходит когда координаты начала линии больше координат ее конца. Есть два варианта устранения этого недостатка: при x2>x1 менять местами координаты или рисовать такие линии залитым прямоугольником отдельно. Мне ближе второй вариант, так как в этом случае скорость рисования таких линий будет выше. Осталось записать четыре возможных случая и соответствующие им координаты прямоугольника, в начале процедуры добавляем следующие строки:
if(y1==y2){if(x1>x2)g.fillRect(x2,y1-w/2,1 x1-x2,w); else g.fillRect(x1,y2-w/2,1 x2-x1,w);return;} if(x1==x2){if(y1<y2)g.fillRect(x1-w/2,y1,w,1 y2-y1); else g.fillRect(x1-w/2,y2,w,1 y1-y2);return;}
Осталось ввести обработку исключительных ситуаций - это возможность деления на ноль при нулевомl и случай когда ширина линии задана нулевая или отрицательная. Обе эти проверки обьединяются в одно условие вывода линии (l>0 && w>0). Полностью работающая функция готова:
public void fillLine(Graphics g,int x1,int y1,int x2,int y2,int w) { if(w==1)g.drawLine(x1,y1,x2,y2);else{ if(y1==y2){if(x1>x2)g.fillRect(x2,y1-w/2,1 x1-x2,w); else g.fillRect(x1,y2-w/2,1 x2-x1,w);return;} if(x1==x2){if(y1<y2)g.fillRect(x1-w/2,y1,w,1 y2-y1); else g.fillRect(x1-w/2,y2,w,1 y1-y2);return;} int a,b,l,lx1,lx2,lx3,lx4,ly1,ly2,ly3,ly4; a=(x2-x1);b=(y2-y1); l=sqrt(100*(b*b a*a)); if(l>0&& w>0){ lx1=(5 b*100*w/2/l x1*10)/10; ly1=(5 y1*10-a*100*w/2/l)/10; lx2=(5 b*100*w/2/l x2*10)/10; ly2=(5 y2*10-a*100*w/2/l)/10; lx3=(5 x1*10-b*100*(w-(w/2)-1)/l)/10; ly3=(5 a*100*(w-(w/2)-1)/l y1*10)/10; lx4=(5 x2*10-b*100*(w-(w/2)-1)/l)/10; ly4=(5 a*100*(w-(w/2)-1)/l y2*10)/10; g.fillTriangle(lx1,ly1,lx3,ly3,lx2,ly2); g.fillTriangle(lx4,ly4,lx3,ly3,lx2,ly2); if(Math.abs(a)>Math.abs(b)){ g.drawLine(lx1,ly1,lx2,ly2); g.drawLine(lx3,ly3,lx4,ly4); }}}}
Линия рисуется текущим цветом, который задается стандартным оператором setColor(). Не забываем, что в приведенной процедуре используется функция sqrt, поэтому для тех кто не любит таскать за собой отдельные функции в примере приведена процедура fillLineI() в которую вычисление квадратного корня интегрировано. Вархиве приведены два готовых примера BoldLineTest и BoldLineDemo. Первый использует интегрированный вариант процедуры fillLineI() и рисует набор статичных линий, такой как на рисунке ниже. Красные черточки показывают, где проходит середина линии.

Второй пример поинтересней, он интерактивен, и выводит на экран линию, толщиной, наклоном и длиной которой можно управлять. Пример называется BoldLineDemo и использует fillLine(), позволяя посмотреть на получившуюся линию в динамике.
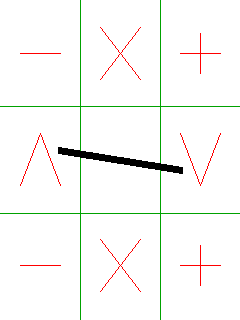
Управляется это чудо цифровыми кнопками или стилусом, при этом решетка три на три на экране соответствует цифровому полю телефона от 1 до 9, тоже три на три. К примеру для поворота линии нужно нажать клавишу 4 или щелкнуть пером в квадрате где изображена стрелка вверх, кресты позволяют выйти из мидлета, плюсы и минусы управляют длиной и толщиной линии. Клавиша 5 или центр экрана возвращает параметры к стандартным. Этот пример позволяет выявить некоторые недостатки реализации предложенного алгоритма, если угол наклона линии близок к 45 градусам при некоторых приращениях толщины визуально толщина линии не изменяется. В принципе устранить этот недостаток возможно - увеличив точность вычислений, но на практике такая потеря точности никому не важна, к примеру в том же PaintNET линии нарисованные под углом 45 градусов с толщиной 6 и 7 визуально не отличаются ;(, как и с толщиной 10 и 11 ;).
Все вышеописанное в виде исходников можно скачатьздесь, в архиве находятся два проекта для NetBeans, исходные тексты и уже готовые приложения для заливки в мобильное устройство. Все примеры работают на любом устройстве с MIDP 2.0, кроме того апплеты проверялись в среде Microemulator.
Автор:Shadowsshot